Количество простых чисел на малых интервалах
С. В. Ситников
Аннотация. Первая, не эмпирическая, формула, для вычисления количества простых чисел на малых интервалах. Формула алгоритма решета Эратосфена. Возможность решать сложные проблемы элементарными методами (количество простых чисел на малых интервалах).
Ключевые слова: интервал, простые числа, решето Эратосфена.
1.
Решето Эратосфена — алгоритм нахождения всех простых чисел до некоторого целого числа.
Выведем формулу алгоритма
Формула (1,1) алгоритма решета Эратосфена
(n) – Номер простого числа
Формула (1,2) вычисления количества простых чисел на интервалах (pn ,m).
Например:
Формула (1,3) вычисления количества простых чисел на малом интервале.
Погрешность вычисления, проблема сложная. И ждёт своего решения.
 берётся только по целым числам
берётся только по целым числам
Но если взять за критерий оценки формулы не величину погрешности вычисления, а количество смены знаков у величин погрешности при вычислениях.
Есть интересный результат. Коэффициент 2,4
k=2,4
(E+-) - Количество смены знаков у величин погрешности при вычислении по формуле (1,4).
Значение в знаменателе берётся только по целым числам
берётся только по целым числам Например: Для интервала (1,x) x=1299709. При коэффициенте
(к)=2,4 (E+-)=151
2.
Расстояние между соседними простыми числами
Дадим четыре определения. 1. Начального отрезка. 2. Базисного числа. 3. Базиса от базисного числа. 4. Особый вид начального отрезка.
2. Базисное число, это простое число (p).
3. Базис от простого числа (p) это все числа кратные (p), без чисел пересечения с предыдущими базисами. Базисное число входит в базис.
4. Особый вид начального отрезка, это отрезок подобный и равный начальному отрезку, и равный начальному отрезку по количеству элементов всех базисов, но с другим расположением базисных чисел.
Отрезок,  можно представить в виде начального отрезка, но с другим начальным расположением базисных чисел. Для этого, начиная с числа
можно представить в виде начального отрезка, но с другим начальным расположением базисных чисел. Для этого, начиная с числа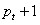 раскладываем числа на простые множители. Меньшее простое число, принимаем за базисное число. Все остальные числа на отрезке, кратные базисному числу, принимаем за его базис. Так же поступаем со следующим составным числом не входящим в предыдущий базис и так далее. В итоге должны получить, из отрезка
раскладываем числа на простые множители. Меньшее простое число, принимаем за базисное число. Все остальные числа на отрезке, кратные базисному числу, принимаем за его базис. Так же поступаем со следующим составным числом не входящим в предыдущий базис и так далее. В итоге должны получить, из отрезка
 можно представить в виде начального отрезка, но с другим начальным расположением базисных чисел. Для этого, начиная с числа
можно представить в виде начального отрезка, но с другим начальным расположением базисных чисел. Для этого, начиная с числа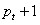 раскладываем числа на простые множители. Меньшее простое число, принимаем за базисное число. Все остальные числа на отрезке, кратные базисному числу, принимаем за его базис. Так же поступаем со следующим составным числом не входящим в предыдущий базис и так далее. В итоге должны получить, из отрезка
раскладываем числа на простые множители. Меньшее простое число, принимаем за базисное число. Все остальные числа на отрезке, кратные базисному числу, принимаем за его базис. Так же поступаем со следующим составным числом не входящим в предыдущий базис и так далее. В итоге должны получить, из отрезка
отрезок особого вида.
Для начала, проверим, может ли существовать отрезок особого вида.
На отрезке поменяем местами базисные числа. То есть из начального отрезка,
поменяем местами базисные числа. То есть из начального отрезка, попытаемся сделать отрезок особого вида.
попытаемся сделать отрезок особого вида. Переменив местами, на начальном отрезке, два базисных числа, изменяться величины и их базисов на начальном отрезке. Имеем:
1, увеличение базиса с большими базисными числами и
2, одновременно уменьшение базиса с меньшими базисными числами.
Наоборот невозможно, потому что это будет возвращение в исходное состояние, возвращение к начальному отрезку.
Изменяются базисы, на одинаковую величину, а базисные числа разные по величине. Значит, в первом случае элементов базиса уйдёт больше, чем прибавиться элементов базиса во втором случае. Количество элементов всех базисов, на отрезке, в сумме уменьшиться
Продолжая менять местами базисные числа. Будем наращивать изменения, в сторону уменьшения, количества элементов всех базисов. Значит. Невозможно создать особый вид начального отрезка, подобный и равный начальному отрезку, но с другим расположением базисных чисел. На отрезке особого вида, количество элементов всех базисов будет меньше. Но это уже будет не отрезок особого вида.
Доказали, не может быть отрезка особого вида.
Литература:
[1] А. И. Бородин. Теория чисел. Киев. 1992
[2] И. Г. Башмакова. Ю. А. Белый. С. С. Демидов. Б. А. Розенфельд. А. П. Юшкевич. Хрестоматия по истории математики. Москва. 1976
[3] Д. Пойа. Математическое открытие. Перевод с английского В. С. Бермана. Под редакцией И. М. Яглома. Москва. 1976.
Сергей Ситников

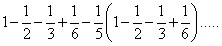




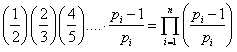


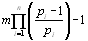
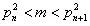




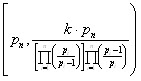



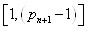


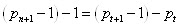


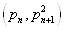
Комментариев нет:
Отправить комментарий