Техническая задача - теорема Ферма
Доказать что уравнение
(1)
при
Не имеет решений в целых числах.
Порядок доказательства теоремы будет следующий.
Рассмотрим три частых случая
1) Первый частный случай
Введём новое обозначение
и получим
(2)
В дальнейшем любое целое число будем обозначать буквой (С) 2=С Z=C 4=C d=C
Так как нас интересует вид числа, а не его величина
Даём (y) в уравнении (2) последовательно значения всех целых чисел начиная с трёх
Определить есть ли при данных значениях


такие целые значения Z=C X=C


такие целые значения Z=C X=C
Которые все вместе являются решением уравнения
по условию
Что бы получить Z=C необходимо выполнение двух условий
(y) и (d) - должны быть одинаковой чётности
Первое и второе условие выполнимо при любом


Докажем это:
Если представить (y) в виде произведения простых сомножителей полученных при факторизации числа (y)




Рассмотрим второй частный случай теоремы
Вернёмся к равенствам (4) и (5)





Что бы было более наглядно, для каждого из трёх случаев значения числа (d) построим таблицу.


при разложении их на простые множители, не будет одинаковых простых множителей кроме двоек. Мы предполагаем, что это двойки.
Проверим, может ли иметь число (d) эти три значения, единственно возможные, при которых (возможна) сохраняется разница между числами
 и
и 
равная двум
Ещё раз напомню (С) это любое целое число
1)
Если представить (y) в виде произведения простых сомножителей полученных при факторизации числа (y)
то число (d) должно быть произведением какой-то части этих сомножителей, например:
И если в числе (y) есть хоть один простой множитель двойка он обязательно должен входить в сомножители числа (d) т.е
. Количество числовых значений (d) равно количеству простых множителей полученных при факторизации числа (y) плюс количество сочетаний из этих простых множителей.
При обязательном условии (y) и (d) должны быть одинаковой чётности.
Значит минус варианты где простые множители или сочетания из простых множителей и(y) разной чётности. Если (y) простое число d=1
Значит минус варианты где простые множители или сочетания из простых множителей и(y) разной чётности. Если (y) простое число d=1
Количество числовых значений (d) равно количеству решений уравнения
в целых числах, при (y) - фиксированное целое число.
Например: y=30
y=2 3 5
d=2 6 10 30
Например: d=6



900+5184=6084 6084=6084.
y=17 d=1
289+20736=21025. 21025=21025
Уравнение примет вид
(3)
Подставим значение
в уравнение (3)
(4)
В первом частном случае мы доказали, что при любомв уравнении (4) это
в левой части уравнения можно получить целое число (С)
Но получить в левой части уравнения (4) целое число (С) необходимо. Но недостаточно. Это целое число (С) должно быть степенью основания (Z)при показателе степени (P)
Но получить в левой части уравнения (4) целое число (С) необходимо. Но недостаточно. Это целое число (С) должно быть степенью основания (Z)при показателе степени (P)
то есть
Но и этого недостаточно получив
необходимо что бы разница между числами
была степенью основания (X)при показателе степени (P)
(4)
(5)
Проверим равенства (4) и (5). Равенства, так как мы предположили, что есть такие значения (x=c) (y=c) (z=c) Которые являются решением уравнения Разделив левые и правые части равенств (4) и (5) на (0.5d) получим
(4)
(5)
Обратим внимание на правые части равенств (4 и 5)
Во первых это числа целые (C) так как мы выше заметили
это необходимое условие для решения квадратного уравнения. Хотя и недостаточное в нашем случае
Разница между ними равна двум
Исходя из этого мы можем утверждать. Что эти два целых числа при разложении их на простые множители, не будут иметь одинаковых, простых множителей. Кроме случая, когда эти числа чётные, они будут иметь одинаковые, простые множители, но только двойки.Вернёмся к равенствам (4) и (5)


Числа (z) и(x) представим в виде произведения простых сомножителей
Полученные значения
подставим в равенства (4) и (5)
В силу того, что числане имеют одинаковых, простых множителей кроме двоек, а простые множители, принадлежащие числу (d) они же и часть простых множителей чисел
повторяются в числах

(p) - раз. Это накладывает ограничения на выбор числа (d)
Каковы же могут быть значения числа (d)?
1)
Каковы же могут быть значения числа (d)?
1)

Где
отсюда
Где
или
Где
Разумеется в первом случае как и в последующих значения

или
и так далее
Нас интересует общий вид числа (d)
Случай когда в число (d) входит отдельный сомножитель двойка

рассматривать не будем отдельно, в ходе проверок покажем, что множитель (2) на результат не влияет.
Что бы было более наглядно, для каждого из трёх случаев значения числа (d) построим таблицу.
Эти три случая охватывают в общем виде все значения числа (d) при которых в числах


при разложении их на простые множители, не будет одинаковых простых множителей кроме двоек. Мы предполагаем, что это двойки.
Проверим, может ли иметь число (d) эти три значения, единственно возможные, при которых (возможна) сохраняется разница между числами
 и
и 
равная двум
Ещё раз напомню (С) это любое целое число
1)

(4)
где если
то
но
Разделим обе части равенства на
(6)
две дроби равны, а тем более равны и их числители , то должны быть равны и знаменатели
проверим
проверим
целые числа
Значит знаменатели в равенстве

не равны
Из целого числа вычитаем целое, а в результате получаем дробное, что невозможно.
Отметим что
Вывод: Число (d) не может иметь значение
В Случае когда
вывод тот же, так как равенство

примет вид
2)
(4)
где
так как
так как
Сделав преобразование видим что разница между числами




Обозначим разницу между числами

подставим в уравнение
и получим после преобразования
(8)
(9)
Обозначим выражение
буквой (e)
e=c целое число
Что бы получить в уравнениях (8) и (9)
целые числа
(8)
(9)

(e) и (d) должны быть одинаковой чётности
Это выполнимо при
1) Если представить число (e) как произведение простых множителей
То число (d) будет совокупность какой-то части этих сомножителей. Например:
2) Если (e)- чётное число . Необходимо ещё одно дополнительное условие, а именно при разложении числа (e) на простые множители, простых множителей двоек (2) должно быть в количестве не менее двух. Один простой множитель двойка (2) обязательно должен входить в простые множители числа (d) Что так же возможно, если (e) - чётное число

чётное число, так как число
всегда чётное
 чётное
чётное
 чётное
чётное
Чётное умножаем на чётное в итоге получаем как минимум в числе (e)


можно получить целое число

(4)
(5)
Сравним уравнения
 и (4) (5)
и (4) (5)
Числа
обладают теми же свойствами что и числа

При проверке не имеет значения какой показатель степени (n), чётное или нечётное число. Значит получаем результат как и во втором частном случае:
Три значения



которая равна двум
при n>2 n – нечётное число


Значит знаменатели в равенстве

не равны
Из целого числа вычитаем целое, а в результате получаем дробное, что невозможно.
Отметим что
Вывод: Число (d) не может иметь значение
В Случае когда
вывод тот же, так как равенство

примет вид
2)
(4)
где
так как
так как
Сделав преобразование видим что разница между числами
не может равняться единице. Так как разница между двумя числами при показателе степени n=2


больше суммы этих чисел, а при возрастании показателя степени разница увеличивается
Вывод, число (d) не может иметь значение
В случае когда
вывод тот же
Равенство неверно
3)
(4)
так как
Разделим обе части равенства на
(7)
(5)
так как
Подставим данные значения
и полученные
в равенства (4 и 5)
(4)
(5)
Значения
Числители равны - равны и знаменатели.
Проверим так ли это
Равенство неверно, оба сомножителя больше еденицы.
Знаменатели не равны - сомножитель
Вывод: Равенство (7) не верно, следовательно число (d) не может иметь значение
В случае, когда
вывод тот же равенство (7) примет вид
Общий вывод для второго частного случая (d) не может иметь значения, при которых разница между числами


может быть равна двум.
При других значениях (d) разница между числами
При других значениях (d) разница между числами


не равна двум что невозможно.
Следовательно, неверны наши предположения, что целое число (c) полученное в уравнении (4) в левой части, есть степень основания (z) при показателе степени (p), или что
Следовательно, неверны наши предположения, что целое число (c) полученное в уравнении (4) в левой части, есть степень основания (z) при показателе степени (p), или что
Значит уравнение
при n>2
n-четное число
n-четное число
Не имеет решений в целых числах.
3)
Возведём обе части уравнения в квадрат

Обозначим разницу между числами
буквой (d)
Значение
подставим в уравнение
и получим после преобразования
(8)
(9)
Обозначим выражение
буквой (e)
e=c целое число
Что бы получить в уравнениях (8) и (9)
целые числа
(8)
(9)
Необходимо:

(e) и (d) должны быть одинаковой чётности
Это выполнимо при
То число (d) будет совокупность какой-то части этих сомножителей. Например:
2) Если (e)- чётное число . Необходимо ещё одно дополнительное условие, а именно при разложении числа (e) на простые множители, простых множителей двоек (2) должно быть в количестве не менее двух. Один простой множитель двойка (2) обязательно должен входить в простые множители числа (d) Что так же возможно, если (e) - чётное число

чётное число, так как число
всегда чётное
 чётное
чётное чётное
чётноеЧётное умножаем на чётное в итоге получаем как минимум в числе (e)
два простых множителя двойки
Доказали что в уравнениях (8) (9) в левых частях при 

можно получить целое число
Преобразовываем уравнения (8) и (9)

(4)
(5)
Сравним уравнения

 и (4) (5)
и (4) (5)Числа
обладают теми же свойствами что и числа
а именно:
1)
1) Это числа целые
2) 1) И разница между ними равна двум. Полагая, что в уравнениях (8и9) в левых частях получили не просто целые числа, а степени оснований Z и X при показателе степени (n) Представляя числа Z и X как произведения простых множителей на которые они расскладываются. Проверяем три значения числа (d)

При проверке не имеет значения какой показатель степени (n), чётное или нечётное число. Значит получаем результат как и во втором частном случае:
Три значения

Невозможны. Но только при этих трёх общих значениях возможна разница между числами


которая равна двум
Удовлетворяющих значений числа (d) нет. Равенства (8,9) неверны.
И ошибочны наши предположения, что числа полученные в уравнениях (8,9) в левых частях есть степени оснований Z и X при показателе степени (n)
Вывод:
Уравнениепри n>2 n – нечётное число
Не имеет решений в целых числах
На основании результатов полученных во втором и третьем частном случае делаем общий вывод:
Уравнение

при n>2

Не имеет решений в целых числах.
Сергей Ситников.



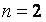
















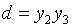






























































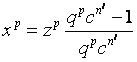

































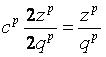

























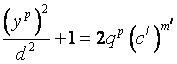















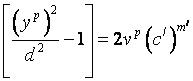





























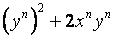













Комментариев нет:
Отправить комментарий